caijizhuo

树状数组

发表于 更新于 分类于
本文字数： 907 阅读时长 ≈ 3 分钟

什么是树状数组

有这样一个问题，给定一个数组，求它的前 $n$ 项和。
1
最简单粗暴的方式，就是一个个加起来，存到一个大小为 $n$ 的数组里面，时间复杂度为 $O(n)$。
但是有一个数变了,由 $b_1$ 变为了 $b_2$，需要更新上述的数组，那么更改的时间复杂度为 $O(n)$，因为为了维护上述数组的性质，需要在变更的数之后的所有数都给加上这个变化 $b_2 - b_1$。求和的时间复杂度为 $O(1)$，因为拿到前缀和之后数组的结果就是答案了。
如果这个数组要被频繁修改，那这种方式效率就很低下了。有没有更快的方式呢？

树状数组的雏形

我们可以做以下处理：
2
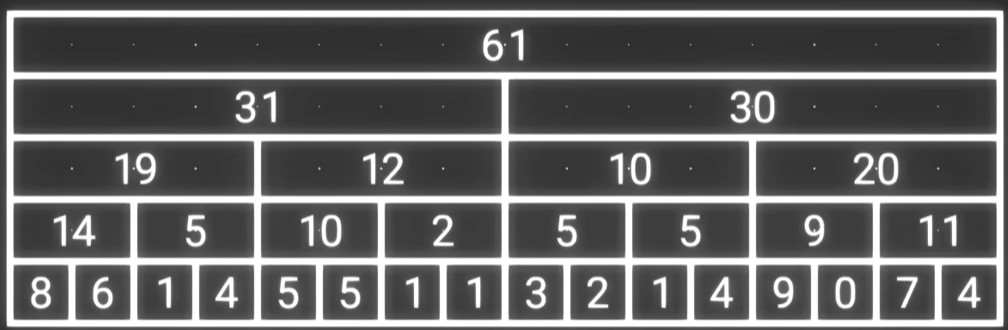
首先将每两个数的和都记录下来，那么求和的时候就可以只求 $(n/2)$ 次了。那么再对第二层的数组再做一个两两求和…次数就变为 $(n/4)$ 次了。以此类推。最后就变成上图这个样子了。如果是这样的话，修改一个数，我们只需要更改 $log_2n$个数就可以了！
仔细观察上述数组，我们发现有一些数字是根本用不上的。第 $i$ 层的偶数个数都用不上。那么他就会变成这个样子：
3
这样空间复杂度就从 $O(n^2)$ 退化为 $O(n)$ 了。这其中的每个数代表一段区间内数字的和。

lowerbits

在介绍树状数组的操作之前，先引入一个函数，这个函数代码如下：

1
2
3
inline int lowerbits(int x) {
    return x & (-x);
}

这个函数的作用是将一个数的二进制格式中最低位的1单独拿出来，比如：

1
2
binary(12) = 00001100   (就展示最低的一个字节)
lowerbits(12) = 00000100  (取最后一个1之后的部分)

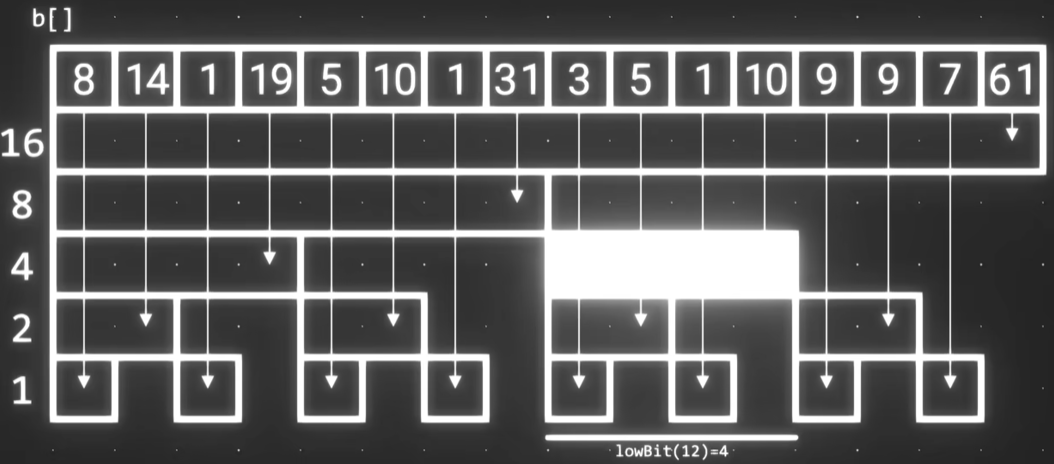
这个函数在树状数组中有什么作用呢？$lowerbits(x)$指代的是下标为 $x$ 的树状数组元素所代表的原数组的区间长度。如图：
4
$lowerbits(12) = 4$ 代表树状数组 $12$ 下标（从 $1$ 开始）所代表的原数组中 $4$ 个数字元素的和。即树状数组元素 $10$ 是原数组 $3,1,2,4$ 的和。

用树状数组的求和

5
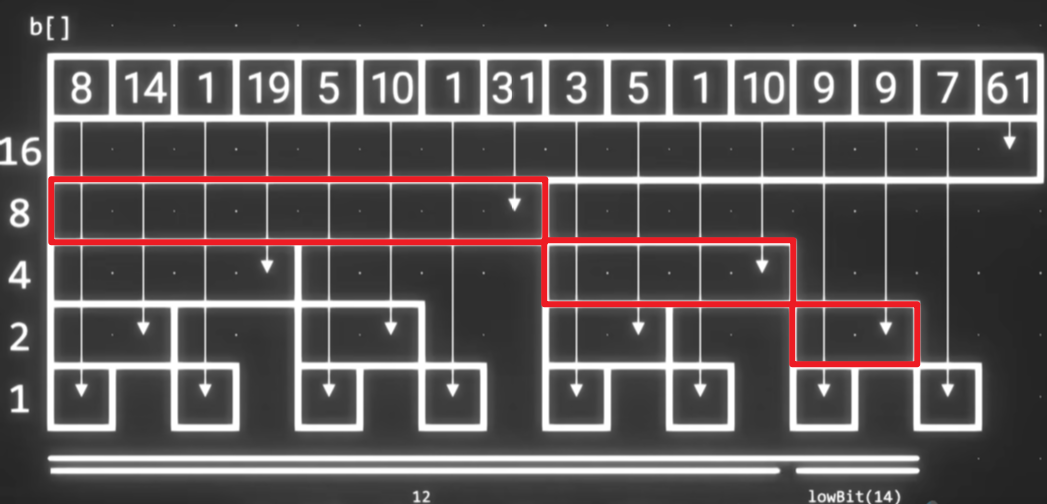
顺着图上的树形结构依次往左上角求和。如图所示。求前 $14$ 项和的值等于 $b[14] + b[12] + b[8]$ 。
代码如下：

1
2
3
4
5
6
7
8
int count(int n) {
    int res = 0;
    while (n > 0) {
        res += b[n];
        n -= lowerbits(n);
    }
    return res;
}

由此可见，利用树状数组求和的时间复杂度是 $O(log_2n)$。

更新树状数组

6
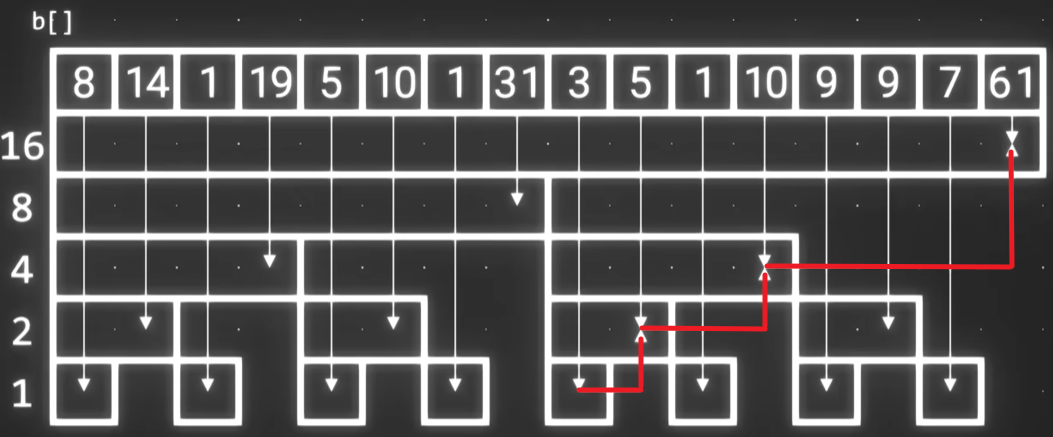
更新操作则是把所有包含了新数字的树状数组元素统统更新一遍，如图中红线所示。顺着树形结构向右上角更新。

1
2
3
4
5
6
7
// delta 是第 i 位数字的变化值
void add(int i, int delta) {
    while (i < N) {
        i += delta;
        i += lowerbits(i);
    }
}

由此可见，更新时间复杂度为 $O(log_2n)$，比最开始的方式快了很多。

初始化树状数组

以下表示中 $a[i]$ 为原数组元素，$b[i]$ 为树状数组元素。

直接初始化为0，并且对每个点调用add。

1
2
3
4
5
void init() {
    for (int i = 1; i < N; i++) {
        add(i, a[i]);
    }
}

时间复杂度 $O(nlog_2n)$。

使用前缀和辅助数组

1
2
3
4
5
6
void init() {
    for (int i = 1; i < N; i++) {
        pre[i] = pre[i - 1] + a[i];
        b[i] = pre[i] - pre[i - lowerbits(i)];
    }
}

这种方式时间复杂度为 $O(n)$，但是要占用额外的空间。