caijizhuo

并查集

发表于 更新于 分类于
本文字数： 683 阅读时长 ≈ 2 分钟

并查集是为了解决什么问题

有10个人，他们之间有错综复杂的关系。如果认定1和2为朋友，2和3也为朋友，那么就认定1和3也是朋友。现在给定两个编号，能否快速知道这两个人是否是朋友？这就是并查集的领域了。

基本思想：

并查集的本质是一个单向且出度为1的图。可以用一个数组来表示，这个数组记录的内容为这个节点所指向的另一个节点的编号。由于这个图出度为1，所以每个元素只唯一的指向另一个元素。而指向的这个节点，我们称为该节点的父节点。
并查集英文叫 unionFind，顾名思义这个数据结构有两个方法，union 和 find。union 用于连接两个集合，find 用于找到这个集合所属的编号。

初始化

只需要把每个节点的父节点设置为自己即可。

1
2
3
4
5
void init() {
    for (int i = 0; i < N; i++) {
        parent[i] = i;
    }
}

所属集合的判断

所属的集合只要一直向上遍历，直到找到祖先为止。祖先的编号就是这整个集合的标志编号。

1
2
3
4
5
6
int find(int i) {
    while (parent[i] != i) {
        i = parent[i];
    }
    return i;
}

关系的建立

如果要把两个节点建立并查集关系，只需要指定一个节点的祖先为另一个节点的父节点就可以了。

1
2
3
4
5
6
7
8
void merge(int a, int b) {
    int x = find(a);
    int y = find(b);
    if (x == y) {
        return;
    }
    parent[x] = y;
}

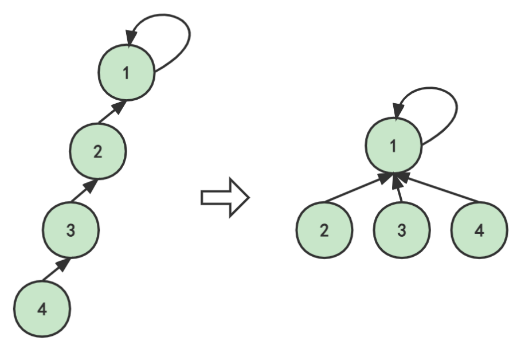
路径压缩

在某些极端情况下，这棵树型结构的集合可能会退化为线性结构，这样的情况下find函数会十分耗时。所以我们可以试着在某些方面优化这个效率。

查找时优化

在查找的过程中就直接将沿途的所有元素都指向根节点，大大的缩短下次查找时的时间。
1

1
2
3
4
5
6
int find(int i) {
    if (i == parent[i]) {
        return i;
    }
    return parent[i] = find(parent[i]); //在第一次查找的时候 将结点直接连到祖先
}

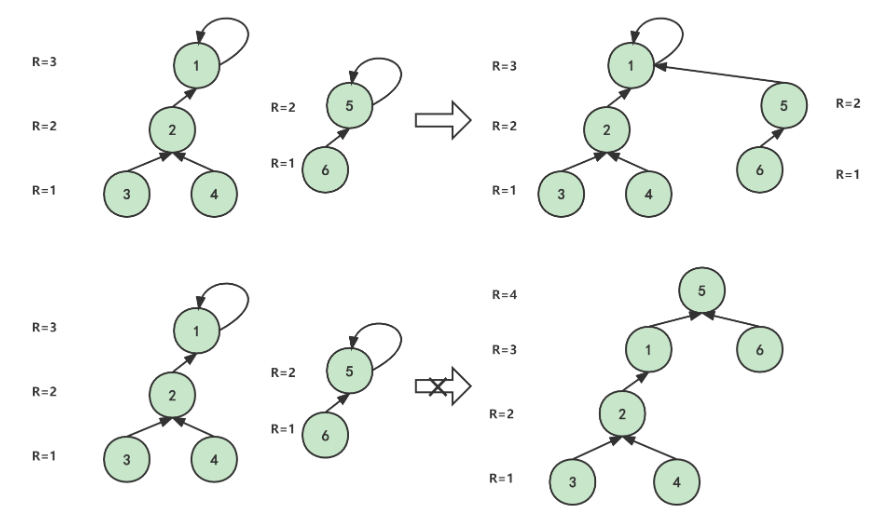
合并时优化

目前的合并是无论如何都让第二个节点的祖先当第一个节点祖先的新祖先，无视了每个集合内树的高度。如果我们记录下树的高度，让较高的树作为新的祖先，较低的树作为它的子节点，可以一定程度的平衡下树的高度。
2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void merge(int a, int b) {
    int x = find(a);
    int y = find(b);
    if (x == y) {
        return;
    }
    // 比高度
    if (rank[x] < rank[y]) {
        parent[x] = y;
    } else {
        parent[y] = x;
        if (rank[x] == rank[y]) {
            rank[x]++;
        }
    }
}