caijizhuo

回文串

发表于 更新于 分类于
本文字数： 1.9k 阅读时长 ≈ 7 分钟

什么是回文串？

回文串是如abcdedcba，abccba这样的字符串，从前往后和从后往前读是一样的结果。
算法逻辑也很简单，从前和从后同时校验一个字符串，如果不相等直接返回失败。时间复杂度为 $O(n)$。

1
2
3
4
5
6
7
8
9
bool check(string s) {
    int len = s.size();
    for (int i = 0; i < len / 2; i++) {
        if (s[i] != s[len - 1 - i]) {
            return false;
        }
    }
    return true;
}

最长回文串问题

给你一个字符串 s，找到 s 中最长的回文子串。
示例：
输入：s = “babad”
输出：“bab”
解释：“aba” 同样是符合题意的答案。

暴力搜索

暴力搜索就是依次判断每个子串，如果是回文串就记录下他的长度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
string longestPalindrome(string s) {
    int len = s.size();
    if (len <= 1) {
        return s;
    }
    int maxlen = 1;
    string res = s.substr(0, maxlen);
    for (int i = 0; i < len; i++) {
        for (int j = 2; i + j <= len; j++) { // j是子串的长度，一种优化手段就是从 maxlen + 1 开始取
            string sub = s.substr(i, j);
            if (check(sub) && j > maxlen) { // 更新最长的回文串信息
                res = sub;
                maxlen = j;
            }
        }
    }
    return res;
}

遍历每个子串的时间复杂度是 $O(n^2)$，检验回文串时间复杂度为 $O(n)$，所以暴力求解的时间复杂度为 $O(n^3)$。

中心扩散法

从每一个位置出发，向两边扩散即可，遇到不是回文串就结束。

举例，s=acdbbdaa时，从s[2]=b开始扩散，是什么步骤呢？

  1. 向左扩散，直到不和原字符相等。
    left = 2, right = 2, cur = 2, len = 1
    acdbbdaa
  2. 向右扩散，直到不和原字符相等。
    left = 2, right = 3, cur = 2, len = 2
    acdbbdaa
  3. 同时向左右扩散，直到左右不相等。
    left = 1, right = 4, cur = 2, len = 4
    acdbbdaa
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
string longestPalindrome(string s) {
    int len = s.size();
    if (len <= 1) {
        return s;
    }
    int left = 0, right = 0, cur = 0;
    string res = "";
    while (cur < len) {
        left = cur, right = cur;
        while (left > 0 && s[left - 1] == s[cur]) { // 向左扩散
            left--;
        }
        while (right < len - 1 && s[right + 1] == s[cur]) { // 向右扩散
            right++;
        }
        while (left > 0 && right < len - 1 && s[left - 1] == s[right + 1]) { // 两边扩散
            left--;
            right++;
        }
        if (right - left + 1 > res.size()) { // 更新结果
            res = s.substr(left, right - left + 1);
        }
        cur++;
    }
    return res;
}

该方法遍历中心点时间复杂度 $O(n)$，扩散的时间复杂度 $O(n)$，总时间复杂度 $O(n^2)$。

动态规划

要判断 $dp[l][r]$ 是否是回文串，只需要知道 $dp[l+1][r-1]$ 是否是回文串就可以了。如果是的话，那么如果 $s[l] == s[r]$，那么就是回文串，否则不是。其中有一种特殊情况，在 $s[l] == s[r]$ 相等时，如果这俩相隔是 $2$， 也可以认为是回文串。
初始化边界条件为所有都是 $false$ ，当 $l==r$ 时为 $true$（单个字符是回文串）。
递推关系式为
$$
dp[l][r] = ((dp[l+1][r-1]\ \ || \ \ j - i <= 2)\ \ && \ \ s[l]==s[r])\ ?\ true : false
$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
string longestPalindrome(string s) {
    int n = s.size();
    vector<vector<bool>> dp(n, vector<bool>(n, false)); // 初始化为都不是
    for (int i = 0; i < n; i++) { // 初始化边界
        dp[i][i] = true;
    }
    string res = s.substr(0, 1);
    for (int i = n - 1; i >= 0; i--) { // 注意遍历顺序，倒着遍历是为了保证依赖的数据是经过计算的
        for (int j = i + 1; j < n; j++) {
            if (dp[i + 1][j - 1] || j - i <= 2) {
                if (s[i] == s[j]) {
                    dp[i][j] = true;
                }
                if (dp[i][j] && j - i + 1 > res.size()) {
                    res = s.substr(i, j - i + 1);
                }
            }
        }
    }
    return res;
}

这种方式时间复杂度为 $O(n^2)$，空间复杂度也为 $O(n^2)$。

Manacher算法

这种算法又被称为“马拉车”，可以用 $O(n)$的时间复杂度解决最长回文字符串问题。这个算法的总框架是，遍历所有的中心点，寻找每个中心点对应的最长回文子串，然后找到所有中心点对应的最长回文子串。但是在时间复杂度上做了优化，使其变成线性。

臂长

为了表述方便，我们定义一个新概念臂长，表示中心扩展算法向外扩展的长度。如果一个位置的最大回文字符串长度为 $2 * length + 1$，其臂长为 $length$。
下面的讨论只涉及长度为奇数的回文字符串。长度为偶数的回文字符串可以在每个字符串之间添加用不到的字符从而达到长度变为 $2n + 1$ 为奇数的目的。
1
从中心扩展的长度即为臂长，$臂长 - 1$ 就是原子串的回文字符串长度。所以问题就变成了求臂长数组。

求原字符串下标

用 $(i - P[i]) / 2$，就是原字符串开头的下标了。例如 $P[6] = 5$，那么原字符串开头下标为 $(6 - 5) / 2 = 0$，所以返回的结果为原字符串的 $[0, 5 - 1]$ 即可。

求每个 P[i]

用 $C$ 表示回文串中心 $Centre$，用 $R$ 表示臂长右半部分下标边界，即 $R = C + P[i]$。$C$ 和 $R$ 对应当前循环中 $R$ 最靠右的回文串（手最长的，能管这个数组到最远的，之所以可以保证复杂度是因为保证 $R$ 不退缩）。
2
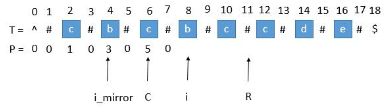
如图，在求 $P[i]$ 时，用 $i_mirror$ 表示要求的第 $i$ 个字符关于 $C$ 对应的下标。我们要求 $P[i]$，用中心扩展法就是向两边伸长。但是可以利用已经求出来的回文串中心 $C$ 的对称性，因为 $P[i_mirror] = 3$，那干脆让 $P[i] = 3$。有以下 $3$ 中情况会导致这个直接赋值不正确：

1. 超出了 R

3
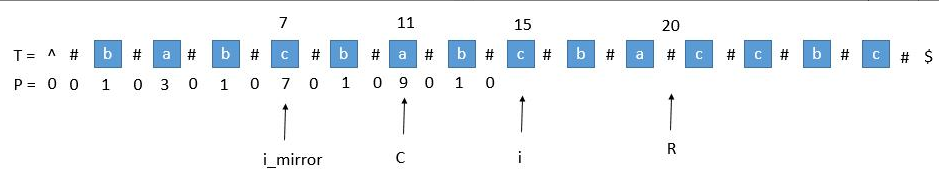
当求 $P[i]$ 时，$P[i_mirror] = 7$，但是却不应该等于 $7$，因为从 $i$ 往后面数 $7$ 个已经等于 $22$ 了，然而 $R$ 才到 $20$，很显然还没有探索到那里。但是可以保证我们一定可以扩展到 $R$（因为对称），所以 $P[i]$ 至少可以为 $5$。剩下的只能中心扩展了。

2. P[i_mirror] 遇到了原字符串左边界

4
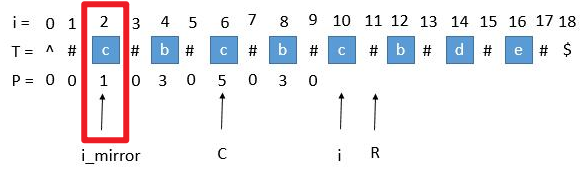
此时 $P[i_mirror] = 1$，但是 $P[i]$ 赋值成 $1$ 是不正确的，原因是 $P[i_mirror]$ 在扩展时首先是 $#=#$ ，之后遇到了边界才终止循环的，但是 $P[i]$ 并没有遇到边界，所以和上面一样继续中心扩展。

3. i == R

这个和情况一很像，将 $P[i] = 0$，之后中心扩展即可。

C 和 R 的更新

一步一步求 $P[i]$， 当求出的 $P[i]$ 的右边界大于当前 $R$ 时，就要更新 $C$ 和 $R$ 了。
5
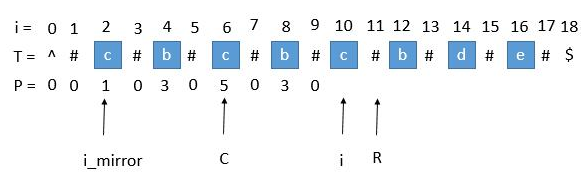
此时 $P[i] = 3$，导致 $R_(new) = 10 + 3 = 13 > 11$，那么 $C = 10, R = 13$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
string longestPalindrome(string s) {
    int len = s.length();
    if (len < 1) {
        return "";
    }
    // 预处理
    string s1;
    for (int i = 0; i < len; i++) {
        s1 += "#";
        s1 += s[i];
    }
    s1 += "#";
    len = s1.length();
    int R = 0;               // 当前访问到的所有回文子串，所能触及的最右一个字符的位置
    int C = 0;               // R对应的回文串的对称轴所在的位置
    int MaxP = 0;            // 最大回文串的回文半径
    int MaxC = 0;            // MaxP对应的回文串的对称轴所在的位置
    vector<int> P(len, 0);   // P[i] 表示以第 i 个字符为对称轴的回文串的回文半径
    for (int i = 0; i < len; i++) {
        if (i < R) {  // 1) 当i在R的左边
            P[i] = min(P[2 * C - i], R - i);
        } else {  // 2) 当i在R的右边
            P[i] = 1;
        }
        // 尝试扩展 P[i]，注意处理边界
        while (i - P[i] >= 0 && // 可以把 P[i] 理解为左半径,即回文串的起始位不能小于 0
               i + P[i] < len && // 同上,即回文串的结束位不能大于总长
               s1[i - P[i]] == s1[i + P[i]]) {  // 回文串特性，左右扩展，判断字符串是否相同
            P[i] += 1;
        }
        // 更新 R, C
        if (P[i] + i - 1 > R) {
            R = P[i] + i - 1;
            C = i;
        }
        // 更新 MaxP, MaxC
        if (MaxP <= P[i]) {
            MaxP = P[i];
            MaxC = i;
        }
    }
    return s.substr((MaxC - MaxP + 1) / 2, MaxP - 1);
}