caijizhuo

KMP算法

发表于 更新于 分类于
本文字数： 935 阅读时长 ≈ 3 分钟

KMP算法是什么

是用来解决字符串匹配的问题。在一个 $str$ 字符串中找到一个子字符串 $sub$，返回索引的位置。
常规能想到的最简单的方式就是一个一个比对，匹配失败的话就向下挪一个位置继续匹配。这样做时间复杂度是 $O(n^2)$。
KMP算法可以在 $O(n)$ 的时间复杂度内解决这个问题。

next数组是什么

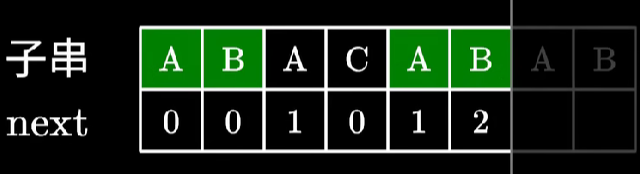
$next$ 数组的本质是寻找子串中“相同前后缀的长度，并且最长”。并且不能是字符串本身。举个例子而言，如下所示：

A B A B C
0 0 1 2 0

第 $1$位 $A$ 只有一个字符，不能是字符串本身，为 $0$；
第 $2$位 $B$ 和 $A$ 比较，不相等，为 $0$；
第 $3$位 $A$ 和 $A$ 比较，相等，所以相同前缀为 $1$；
第 $4$位 $B$ 和前缀为 $1$ 后的 $B$ 比较，相等，和前缀组成了 $AB$ 的相同模式的串，所以相同前缀为 $2$；
第 $5$ 位 $C$ 和前缀为 $2$ 后的 $A$ 比较，不相等，和前缀长度为 $0$ 的比，相同前缀为$0$；
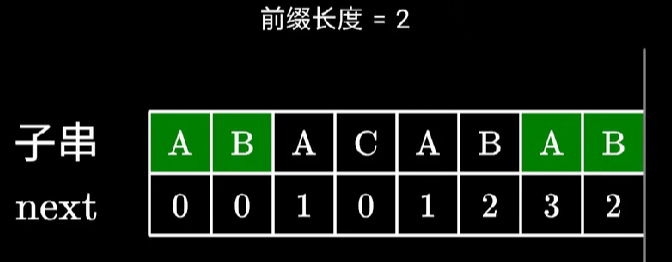
关于最长前缀的理解是，如下图所示。
next
最后一位的 $A$ 很显然可以和 $ABA$ 组成长度为 $3$ 的相同前缀，也可以自己 $A$ 组成长度为 $1$ 的相同前缀。这种情况下选择较大的那个值。

求解next数组

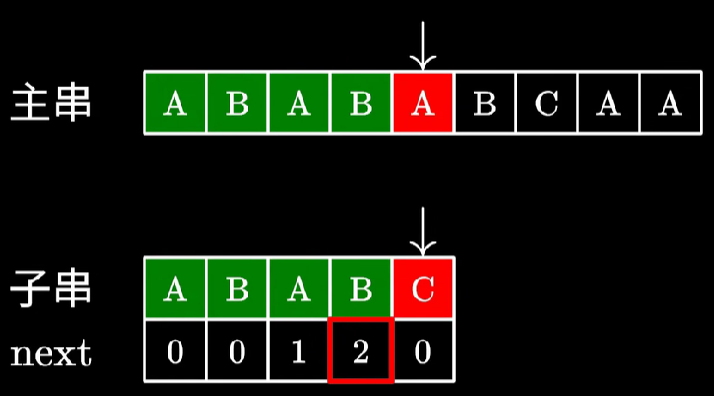
$next$ 数组求解的本质是动态规划。假设我们已经知道当前数字的共同前后缀了，如下图所示。
1
接下来求第 $i$ 位的 $next$ 数组，分为两种情况。

  1. 下一位也和前缀相等
    那就很明显等于 $next[i - 1]$ 加上 $1$。
  2. 下一位和前缀不相等
    这里不是直接等于 $0$ 哦。如下图所示
    2
    虽然 $ABAB$ 和 $ABAC$ 并不相等，但是也不能直接设为 $0$。因为这个新来的 $B$ 可以和前面的 $A$ 组成 $AB$，达到 $2$ 的长度。那么这个数难道要暴力求解吗？其实不然。此时第 $i - 1$ 位的 $next$ 的可利用的值在前缀的 $next$ 数组中可以得到答案，在本图中为 $next[2]$，即是 $1$。此时修改前缀长度为 $next[2]$，则又回到了最开始的状况，匹配长度为 $1$ 并且匹配下一位，下一位 $B$ 相等，所以 $next[i]$ 为 $1 + 1 = 2$。
    代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
vector<int> buildNext(string sub) {
    vector<int> next;
    next.push_back(0);
    int prefix_len = 0;
    int i = 1; // 处理的索引，不会后退，以保证时间复杂度为O(n)
    while (i < sub.size()) {
        if (sub[i] == sub[prefix_len]) { // 下一位相等，next数组数值+1
            prefix_len++;
            next.push_back(prefix_len);
            i++;
        } else { // 下一位不相等
            if (prefix_len == 0) {
                next.push_back(prefix_len); // 目前没有相等的，就是0了
                i++;
            } else {
                prefix_len = next[prefix_len - 1]; // 有不为0的前缀选择，继续回到开始状况
            }
        }
    }
    return next;
}

next数组在KMP中的应用

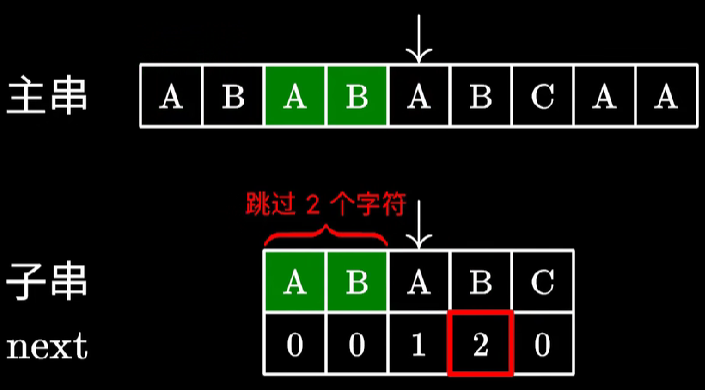
KMP算法在匹配失败的时候，回去看最后失败的字符前一个字符所对应的 $next$ 值。$next$ 数组中的值是什么作用呢？它代表我们可以“跳过匹配”的字符数量。
3
4
这样就可以保证匹配的 $i$ 不向后退，达到时间复杂度 $O(n)$ 的目的。
代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int kmp(string s, string sub) {
    vector<int> next = buildNext(sub);
    int i = 0; // 主串指针
    int j = 0; // 子串指针
    while (i < s.size()) {
        if (s[i] == sub[j]) { // 匹配，指针后移
            i++;
            j++;
        } else if (j > 0) { // 匹配失败，但是next跳过了一些字符继续匹配
            j = next[j - 1];
        } else { // 子串第一个字符就匹配失败
            i++;
        }
        if (j == sub.size()) {
            return i - j; // 成功，返回初始下标
        }
    }
    return -1; // 失败
}