函数调用时发生了什么
在 C 语言中,函数调用在底层汇编究竟发生了什么呢?示例如下:
1
2
3
4
5
6
7
8
9
10
| int add(int a, int b) {
return a + b;
}
int main() {
int a = 9;
int b = 10;
int c = 11;
int d = add(a, b);
return 0;
}
|
对上面这个文件编译的结果进行反汇编,这两个函数的反汇编结果如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| @└────> # objdump -d a.out
0000000000400536 <add>:
400536: 55 push %rbp // rbp 是被调用者保存,把上一个函数的栈基址保存
400537: 48 89 e5 mov %rsp,%rbp // 将栈顶设为新的栈基址,至此本函数的栈已经初始化好了
40053a: 89 7d fc mov %edi,-0x4(%rbp) // 将局部变量 a 放在栈上
40053d: 89 75 f8 mov %esi,-0x8(%rbp) // 将局部变量 b 放在栈上
400540: 8b 55 fc mov -0x4(%rbp),%edx
400543: 8b 45 f8 mov -0x8(%rbp),%eax
400546: 01 d0 add %edx,%eax // 相加两个数,并将返回值放在 eax
400548: 5d pop %rbp // 恢复 上一个函数的栈基址
400549: c3 retq // 恢复 rip 寄存器,返回调用该函数的下一条指令地址
000000000040054a <main>:
40054a: 55 push %rbp
40054b: 48 89 e5 mov %rsp,%rbp // 同上,栈初始化
40054e: 48 83 ec 10 sub $0x10,%rsp // 栈的空间先摆好
400552: c7 45 fc 09 00 00 00 movl $0x9,-0x4(%rbp) // a 初始化
400559: c7 45 f8 0a 00 00 00 movl $0xa,-0x8(%rbp) // b 初始化
400560: c7 45 f4 0b 00 00 00 movl $0xb,-0xc(%rbp) // c 初始化
400567: 8b 55 f8 mov -0x8(%rbp),%edx
40056a: 8b 45 fc mov -0x4(%rbp),%eax
40056d: 89 d6 mov %edx,%esi // 第二个入参,因为从右往左放入
40056f: 89 c7 mov %eax,%edi // 第一个入参
400571: e8 c0 ff ff ff callq 400536 <add>
400576: 89 45 f0 mov %eax,-0x10(%rbp) // 返回值放入 d
400579: b8 00 00 00 00 mov $0x0,%eax // return 0
40057e: c9 leaveq
40057f: c3 retq
|
可以看到,在函数调用时,发生了不同函数栈的切换。其中涉及到一些相关汇编指令。
汇编指令中的 push pop call 和 ret
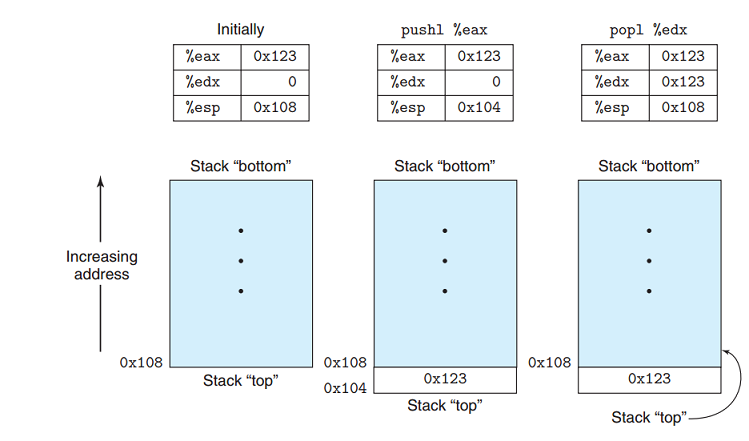
push 和 pop

如上图所示,%rbp 寄存器和 %rsp 寄存器表示这一个栈的 “基址” 和 “栈顶”。因为栈是从高向低生长的,所以基址在栈顶上面。push 操作相当于,先将栈顶向下移动(因为存数据是向 %rsp 指向的位置写数据,而 %rsp 指向的是目前已有的栈顶数据),再将数据写入。pop 操作则相反。通过这两个寄存器,可以维护一个栈的存在。调用函数设计到栈的切换,所以就是通过改变这两个寄存器的值来达到切换的。
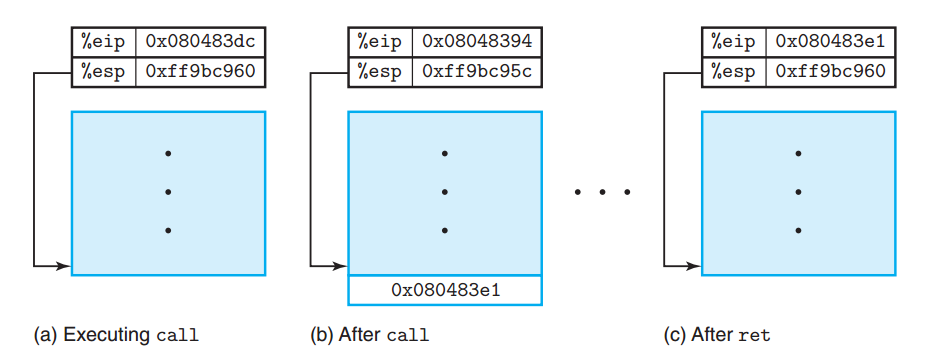
call 和 ret

如上图所示,调用函数涉及到执行指令的切换。将要执行的下一条指令又由 %rip 寄存器指出。
call 指令可以改变 %rip 寄存器的值:将 call 汇编指令的下一条指令地址 push 到栈中,之后改变 %rip 为 call 的指令地址。
ret 指令也可以改变 %rip 寄存器的值:将栈顶元素 pop 给 %rip,将其改为之前 call 时存的下一条要执行的指令地址。
二叉树遍历示例
那么操作系统这一系列操作对于我们将递归算法转换为迭代算法有什么启发吗?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| vector<int> ret;
void helper(TreeNode* root) {
if (root == nullptr) {
return;
}
helper(root->left);
ret.push_back(root->val);
helper(root->right);
}
vector<int> inorderTraversal(TreeNode* root) {
ret.clear();
helper(root);
return ret;
}
|
上面是二叉树中序遍历的递归写法,非常简洁。其中可以看到在递归函数 helper 中,又调用了两次 helper。我们知道每次调用 helper,都有它自己的调用栈。那么我们向迭代转换时,就要注意不能让他们的调用栈互相冲突。那么我们可以自己定义一个状态变量,用来存储当前执行的函数栈。除此之外,还要知道当前栈执行到本次函数的哪个位置(%rip)。两次 helper 的执行,可以将整个调用结构分为三部分:
- 执行 helper(root->left) 之前
- 执行 helper(root->left) 之后,执行 helper(root->right) 之前
- 执行 helper(root->right) 之后
我们定义一个 state 结构体,用于充当存储函数局部变量和执行位置。改写后函数如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| typedef struct state {
TreeNode* node;
int stage;
};
vector<int> inorderTraversal(TreeNode* root) {
stack<state> s;
vector<int> ret;
s.push({root, 0});
while (!s.empty()) {
state top = s.top();
s.pop();
if (top.stage == 0) {
if (top.node == nullptr) {
continue;
}
s.push({top.node, 1});
s.push({top.node->left, 0});
} else if (top.stage == 1) {
s.push({top.node, 2});
ret.push_back(top.node->val);
s.push({top.node->right, 0});
} else if (top.stage == 2) {
}
}
return ret;
}
|