1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
| #include<sys/types.h>
#include<sys/socket.h>
#include<netinet/in.h>
#include<arpa/inet.h>
#include<assert.h>
#include<stdio.h>
#include<unistd.h>
#include<errno.h>
#include<string.h>
#include<fcntl.h>
#include<stdlib.h>
#include<sys/epoll.h>
#include<pthread.h>
#define MAX_EVENT_NUMBER 1024
#define BUFFER_SIZE 10
int setnonblocking(int fd)
{
int old_option = fcntl(fd, F_GETFL);
int new_option = old_option | O_NONBLOCK;
fcntl(fd, F_SETFL, new_option);
return old_option;
}
void addfd(int epollfd, int fd, bool enable_et)
{
epoll_event event;
event.data.fd = fd;
event.events = EPOLLIN;
if (enable_et)
{
event.events |= EPOLLET;
}
epoll_ctl(epollfd, EPOLL_CTL_ADD, fd, &event);
setnonblocking(fd);
}
void lt(epoll_event* events, int number, int epollfd, int listenfd)
{
char buf[BUFFER_SIZE];
for (int i = 0; i < number; i++) {
int sockfd = events[i].data.fd;
if (sockfd == listenfd) {
struct sockaddr_in client_address;
socklen_t client_addrlength = sizeof(client_address);
int connfd = accept(listenfd, (struct sockaddr*)&client_address, &client_addrlength);
addfd(epollfd, connfd, false);
printf("connect fd:%d listenfd=%d\n", connfd, listenfd);
} else if (events[i].events & EPOLLIN) {
printf("event trigger once\n");
memset(buf, '\0', BUFFER_SIZE);
int ret = recv(sockfd, buf, BUFFER_SIZE - 1, 0);
printf("socket fd:%d listenfd=%d\n", sockfd, listenfd);
if (ret < 0) {
close(sockfd);
continue;
}
printf("get %d bytes of content: %s\n", ret, buf);
} else {
printf("sth else happend\n");
}
}
}
void et(epoll_event* events, int number, int epollfd, int listenfd)
{
char buf[BUFFER_SIZE];
for (int i = 0 ; i < number; i++) {
int sockfd = events[i].data.fd;
if (sockfd == listenfd) {
struct sockaddr_in client_address;
socklen_t client_addrlength = sizeof(client_address);
int connfd = accept(listenfd, (struct sockaddr*)&client_address, &client_addrlength);
addfd(epollfd, connfd, true);
} else if (events[i].events & EPOLLIN) {
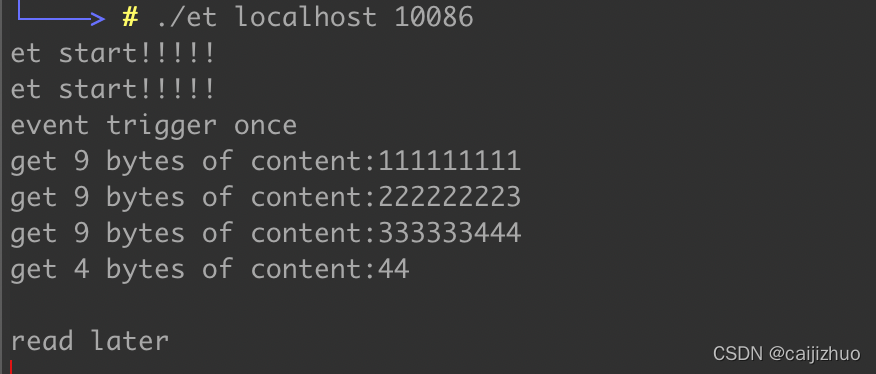
printf("event trigger once\n");
while (1) {
memset(buf, '\0', BUFFER_SIZE);
int ret = recv(sockfd, buf, BUFFER_SIZE - 1, 0);
if (ret < 0) {
if ((errno == EAGAIN) || (errno == EWOULDBLOCK)) {
printf("read later\n");
break;
}
close(sockfd);
break;
} else if (ret == 0) {
close(sockfd);
} else {
printf("get %d bytes of content:%s\n", ret, buf);
}
}
} else {
printf("nothing happend\n");
}
}
}
int main(int argc, char* argv[])
{
if (argc <= 2) {
printf("usage: %s ip_address port_number\n", basename(argv[0]));
return 1;
}
const char* ip = argv[1];
int port = atoi(argv[2]);
int ret = 0;
struct sockaddr_in address;
bzero(&address, sizeof(address));
address.sin_family = AF_INET;
inet_pton(AF_INET, ip, &address.sin_addr);
address.sin_port = htons(port);
int listenfd = socket(PF_INET, SOCK_STREAM, 0);
assert(listenfd >= 0);
ret = bind(listenfd, (struct sockaddr*)&address, sizeof(address));
assert(ret != -1);
ret = listen(listenfd, 5);
assert(ret != -1);
epoll_event events[MAX_EVENT_NUMBER];
int epollfd = epoll_create(5);
addfd(epollfd, listenfd, true);
while(1) {
int ret = epoll_wait(epollfd, events, MAX_EVENT_NUMBER, -1);
if (ret < 0) {
printf("epoll fail\n");
break;
}
et(events, ret, epollfd, listenfd);
}
close(listenfd);
return 0;
}
|